JSONの時系列データがたくさん手に入りました。なにせJSONなんだし、JavaScriptを使ってブラウザにインタラクティブなグラフを簡単に描けそうな気がします。そこでとりあえず折れ線チャートを描くことにしました。むかしjQuery用のFlotというライブラリを使ったことがあったので、今回もこれを使おうと思ったのですが、完全に使い方を忘れていた!そういえば、むかし使ったときも、API.txtという英文がだらだら書かれたテキストファイルしかドキュメントがなくて面倒だったのを忘れていました。そこで今回は備忘録を残しておくことにしたしだい。
なお、Flotはべつに時系列の折れ線チャートを描くためのライブラリではないので、ほかにもいろいろなチャートが描けるはずですが、とくに調べていないので知りません。あくまでも時系列データの折れ線チャートを描くことが目標の備忘録です。
下準備
描画したい時系列データは、こんな1つの配列として用意します。
mydata = [[1309446000000, 6],
[1312124400000, 9],
[1314802800000,18],
[1317394800000,23],
[1320073200000,27],
[1322665200000,27],
[1325343600000,31],
[1328022000000,35],
[1330527600000,38],
[1333206000000,44],
[1335798000000,49],
[1338476400000,50]]要素である長さ2の配列が、それぞれ [日時, データ値] を表しています。
第一要素の日時が 1309446000000 のようなでっかい数値なのは、UNIX時間をミリ秒単位で表したものだからです。これ以外の書式でFlotに日時を指定するすべはありません。もし「2012年7月4日の値は12で、2012年7月5日の値は0で、……」だったら、 [[1341327600000, 12], [1341414000000, 0], ...] という配列を用意するわけです。Gaucheで用意するならこんな感じ。( construct-json-string は、S式からJSON表記の文字列をよろしく作ってくれる関数です。)
(use srfi-19)
(use gauche.sequence)
(use rfc.json)
(define (localtime->jstime str)
(* 1000
(time->seconds
(date->time-utc
(string->date str "~Y年~m月~d日")))))
(define mydata
#(#("2012年7月4日" 12) #("2012年7月5日" 0)))
;; (construct-json-string mydata) の出力ではだめ
(construct-json-string
(map-to <vector>
(lambda (v) (vector (localtime->jstime (ref v 0)) (ref v 1)))
mydata))ちなみに、日時に限らず、Flotが受け付けてくれる値データは数値のみです。文字列の値データは与えないこと。
とりあえず描く
おおざっぱなノリとしては、HTMLページ中にグラフの出力場所を作っておいて、 jQuery.plot(出力場所, [データ列], オプション) とすれば、それっぽい折れ線チャートができるという仕組みです。
<html>
<head>
<script language="javascript" type="text/javascript"
src="http://code.jquery.com/jquery-latest.js"></script>
<script language="javascript" type="text/javascript"
src="flot/jquery.flot.js"></script>
</head>
<body>
<div id="placeholder" style="width:600px;height:300px;"></div>
</div>
<script>
var options = { xaxis :
{ mode : "time"}
};
var mydata = [
[1309446000000, 6],
[1312124400000, 9],
[1314802800000,18],
[1317394800000,23],
[1320073200000,27],
[1322665200000,27],
[1325343600000,31],
[1328022000000,35],
[1330527600000,38],
[1333206000000,44],
[1335798000000,49],
[1338476400000,50]
];
$.plot($("#placeholder"), [mydata], options);
</script>
</body>
</html>
描画する場所は、この例では <div id="placeholder" style="width:600px;height:300px;"></div> です。このように、必ず縦と横の長さを明示してやります。
スクリプトから、この描画場所を参照するときは、この例のようにセレクタを jQuery() に渡してjQueryオブジェクトを作り、それを渡します。グラフを表示するだけなら、 $.plot("div#placeholder",...) のようにセレクタを直接指定するだけでもかまわないようですが、あとでjQueryオブジェクトの bind() メソッドを使ってインタラクティブな機能を付け足したいので、jQueryオブジェクトにしておきます。
$.plot() の3つ目の引数である options は、上記の例では {xaxis : { mode : "time"}} です。「x軸( xaxis )のデータの種類( mode )は日時( "time" )だよ」と意味です。こう指定すれば、元データの第一要素が日時データとして解釈され、x軸にそれっぽいラベルが適当な間隔でふられます。描画の際のオプションはほかにもいろいろ指定できますが、時系列データをプロットするときによく使いそうなものだけメモしておきます。ほかは公式のテキストで「Customizing the axes」とか検索して調べる。
| 項目 | オプション | 値の例 | 意味 |
|---|
| xaxis | mode | "time" | x軸の値を日時とみなす。 |
| timeformat | "%y/<br>%m" | 日時ラベルの書式。htmlタグ使える。 |
| ticks | 10 | x軸に表示するラベルの数。画面に入らないと適当にふり直してくれる。 |
| [] | x軸にラベルを表示しない。 |
| tickSize | [1, "day"] | 1日おきにラベルをふる。 |
| grid | clickable | true | グラフをクリックしてイベント飛ばせるようになる。 |
| hoverable | true | グラフにマウスオーバーでイベント飛ばせるようになる。 |
あらかじめ用意するデータ列 mydata はそもそも配列ですが、それをさらに [mydata] のように配列で括ってから $.plot() に渡している点に注意。この配列に複数のデータ列 [mydata1, mydata2] を指定すれば、ひとつのチャートに複数の折れ線を重ねてプロットできます。
var mydata1 = [
[1309446000000, 6],
[1312124400000, 9],
... // 長いので省略
];
var mydata1 = [
[1309446000000, 0],
[1312124400000, 10],
... // 長いので省略
];
$.plot($("#placeholder"), [mydata1, mydata2], options);
さて、この例のように $.plot() に引数として描画の際のオプションを渡すのでは、それぞれの線の色を好みに応じて変えたり凡例を指定したりすることはできません。次はその方法です。
凝ったグラフ用にデータを準備する
ここまでの例では、jQuery.plot()の第二引数に、 [[日時,データ], ...] というカタチをしたデータ列そのものを指定してました。実はこれは手抜きなやり方で、本当はデータ列とそのメタ情報をJavaScriptのオブジェクトとしてまとめて指定します。
var myseriese1 = {
label : "rapid", // データ列の名前
data : mydata1, // データ列
color : "rgba(255, 0, 0, 0.8)", // チャートの色
... // ほかはドキュメント参照
}
var myseriese2 = {
label : "human", // データ列の名前
data : mydata2, // データ列
color : "#rgba(255, 0, 0, 0.8)". // チャートの色
...
}
$.plot($("#placeholder"),
[myseriese1, myseriese2],
$.extend(true, {}, options, { legend : { position : "nw" }})); color は、まあ、線の色です。 label のほうは、指定した文字列が凡例に使われます。凡例は、デフォルトではグラフ領域の右上に表示されますが、これを左上に移動したいときは、この例のようにしてオブジェクト options を拡張( jQuery.extend() )してやります。 "nw" は「北西」ですね。
外部のファイルからJSONデータを読み込む
Flotがデータ列としてとるオブジェクトは、見ての通りまんまJSONです。そこで外部のファイルに保存してあるJSONのデータを読み出してグラフにしたい。これにはjQueryの jQuery.getJSON() メソッドを使います。
JSONがFlotのデータ列として適当な形式になってるとは限らないので、たとえばこんな内容のファイル mydata.json があったとしましょう。
[{
"entry" : {
"code" : "rapid",
"title" : "うさぎ",
"data" : [[1309446000000, 6],
... // 省略
[1338476400000,50]]
}
},
{
"entry" : {
"code" : "human",
"title" : "ヒト",
"data" : [[1309446000000, 6],
... // 省略
[1338476400000, 1]]
}
},
... // 省略
] "data" をデータ列として使い、 "title" を凡例用のラベルとして使い、チャートを書きたいとします。
var options = { xaxis: { mode: "time" },
legend : { position : "nw" }
};
$.getJSON("mydata.json", function (json) {
var target1 = getEntry(json, "rapid");
var target2 = getEntry(json, "human");
var plotdata = [{label : target1.title , data : target1.data},
{label : target2.title , data : target2.data}];
$.plot($("#placeholder"), plotdata, options);
});
function getEntry (json, codestr) {
i=0;
while (i < json.length) {
if (json[i].entry.code == codestr) {
return json[i].entry}
++i}
return false;
};
出力は前の例とほとんど一緒なので省略。
インタラクティブなグラフにしたい
いままでの要領でまず素朴なグラフを描き、その描画領域のjQueryオブジェクト(いまの例では $("#placeholder") )の bind() メソッドを使うことで、グラフにさまざまな機能を付け足すことができます。たとえば、上の例で $.getJSON() に渡している関数の中身に以下のコードを付け足すことで、「グラフ上をマウスでドラッグした範囲にズーム」という芸当ができるようになります( jquery.flot.selection.js が必要なのでHTMLファイルのヘッダ部分に呼び出しを追加しておくこと)。
$("#placeholder").bind("plotselected", function (event, ranges) {
$.plot($("#placeholder"), plotdata,
$.extend(true, {}, options, {
xaxis: { min: ranges.xaxis.from, max: ranges.xaxis.to }
}));
});
bind の第一引数に指定できるイベントには、この例で使った "plotselected" のほか、 "plothover" や "plotclick" などがあります。名前のとおり、選択した領域に対するアクション、マウスオーバー時のアクション、マウスクリック時のアクションを関数として指定できます。ほかにもありそうだけど調べてません。このへんはドキュメントにはあまり解説がなくて、むしろ公式サンプルで遊びながらソースを参照しましょう。下の画面程度の完成度でよければ、サンプルからのコピペ駆動でそれほど苦もなく実現できます。
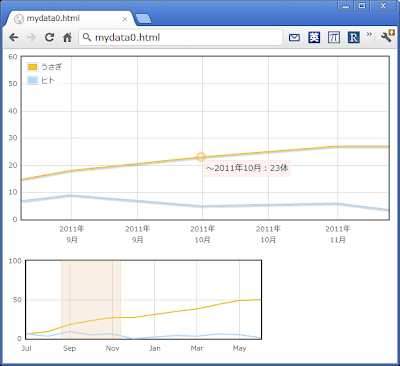
<html>
<head>
<script language="javascript" type="text/javascript"
src="http://code.jquery.com/jquery-latest.js"></script>
<script language="javascript" type="text/javascript"
src="flot/jquery.flot.js"></script>
<script language="javascript" type="text/javascript"
src="./flot/jquery.flot.selection.js"></script>
</head>
<body><div>
<div id="placeholder" style="width:600px;height:300px;"></div>
<br>
<div id="overview" style="width:400px;height:150px"></div>
</div>
<script>
var options = { xaxis: { mode: "time", timeformat: "%y年<br>%m月"},
legend : { position : "nw" },
selection: { mode: "x" },
grid: { hoverable: true, clickable: true }
};
$.getJSON("mydata.json", function(json) {
var target1 = getEntry(json, "rapid");
var target2 = getEntry(json, "human");
var plotdata = [{label: target1.title , data: target1.data},
{label: target2.title , data: target2.data}];
var plot = $.plot($("#placeholder"), plotdata, options);
var overview = $.plot($("#overview"), plotdata, {
series: {
shadowSize: 0
},
legend: { show: false },
xaxis: { mode: "time" },
yaxis: { ticks: 1, min: 0, autoscaleMargin: 0.1 },
selection: { mode: "x" }
});
var previousPoint = null;
$("#placeholder").bind("plothover", function (event, pos, item) {
if (item != null && previousPoint != item.datapoint) {
previousPoint = item.datapoint;
$("#tooltip").remove();
var d = new Date(item.datapoint[0]),
Y = d.getFullYear(),
M = d.getMonth() + 1,
r = item.datapoint[1].toFixed();
showTooltip(item.pageX, item.pageY,
"~" + Y + "年" + M + "月" + ":" + r + "体");
} else {
$("#tooltip").remove();
previousPoint = null;
}
})
$("#placeholder").bind("plotselected", function (event, ranges) {
var plot = $.plot($("#placeholder"), plotdata,
$.extend(true, {}, options, {
xaxis: { min: ranges.xaxis.from, max: ranges.xaxis.to }
}));
overview.setSelection(ranges, true);
});
$("#overview").bind("plotselected", function (event, ranges) {
plot.setSelection(ranges);
});
});
function getEntry (json, codestr) {
var i=0;
while (i < json.length) {
if (json[i].entry.code == codestr) {
return json[i].entry}
++i}
return false;
};
function showTooltip(x, y, contents) {
$('<div id="tooltip">' + contents + '</div>').css( {
position: 'absolute',
display: 'none',
top: y + 5,
left: x + 5,
border: '1px solid #fdd',
padding: '2px',
'background-color': '#fee',
opacity: 0.80
}).appendTo("body").fadeIn(200);
};
</script>
</body>
</html>