そういえば、Ligetiが死んだっていうニュースを最近聞いた。何枚かCDを持ってるけど、ふだん聞いているのはピアノ練習曲集ばかりだし、散漫にいくつかの作品を聞いているだけだったせいか一貫した「らしさ」みたいなものをさっぱり感じられず、あまり思い入れがなかった。思い入れがないと持っているCDのライナーノーツさえ読まないので、どんな背景を持った作曲家なのかもよく知らない。まあ、それでもピアノ練習曲集だけは面白かったので、たまに思い出したように聴いていた。多少の調声が感じられる曲があるのも聴きやすかった。
死んだっていうニュースをきっかけに、ピアノ練習曲集(Naxos 8.555777)のライナーノーツとWikipedia(日本語)だけ読んでみた。けっこう面白いオヤジだったらしい。
改めてこういう記事を読むと、いろいろ府に落ちるところがある。どうやら作風はころころ変わってて、ピアノ練習曲はごく最近のライフワークだったのね。Conlon Nancarrowからの影響についてはライナーノーツでも触れられてたので、確かなんだろう。っていうか、ぼく自身、NancarrowのCDはLigetiよりもはるかによく聴いてる。つまり、ぼくはそういうの(自分では勝手に「パラパラした感じ」って言ってますが)が好きってことで、だからLigetiでもピアノ練習曲だけはよく聴いてたんだろう。
たぶん、前期の楽曲のCDはこれからも滅多に聴かないね。音楽には、作者や演奏者と時代を共有している聴者にとっては極端に有意味なものがあると思うんだけど(Free Jazzとか、Zeppelinの初期とか。それがつまらないという意味ではなく、当時のムーブメントとか気分とかいうやつを共有していなければ正直よく理解できないほどの評価をされているんじゃないか、という意味)、Ligetiの初期の楽曲にもそういうのがありそう。晩年のピアノ練習曲も同じなのかもしれないけど、少なくともぼくには共有できる何かがあるっぽい。だから聴く。ようするに趣味の問題といってしまえばそれまでなわけで。
2006/06/25
2006/06/23
どんな分野にも売り上げランキングというのがあって、なにかしらモノを作って販売している人間にとっては気になってしかたがない情報なわけですよ。とくに競合が多い場合は。書籍もその例に漏れないんだけど、レコード業界におけるオリコンのような存在がないから、信用できるランキングというものがない(ここで「信用できる」というのは、少なくともエンドユーザやマスコミや同僚や上司や同業他社といった他者に対するアピールに活用する場合を想定している)。その結果、みんな、主に次のようないろんな意味で偏りがあるランキング情報に頼っている。
もうどうしょうもないのは、1番目のランキングで高水準にある書目を見て、それが日本中でベストセラーになっているかのごとく勘違いしている場合。バカだろ。まあ、そんなケースは出版社の中にいない限りお目にかかれないけど、中にいるとしばしばお目にかかる。
2番目のランキングは、もう少し現実を反映している。でも、書店っていうのは、読者として意識している以上に得意分野と不得意分野の売り上げ差があるものだと思う。だから、特定の書店から報告されるランキングだけ目にして「○○の本は売れている」と言い放つ人は苦手だ。
いちばんイラってくるのは、3番目のランキングだけをもってあーだこーだ言われるケースである。つーか、あの「Amazonランキング」って何さ。1時間ごとに更新されるようだけど、Amazonランキングが1000だったら、少なくともその時間帯には日本で1000番目に売れている本なのか? とまあ、そういう感想が(出版社にいる以上)当然だと思うんだけど、これがぜんぜん当然じゃない。瞬間値にすぎないAmazonランキングをやたらに気にしたり、なんか適当なキーワードで検索して一番先頭に表示されることに意味を見出そうとする。そのような場当たり的な検証からは、その書籍が市場で評価されているかどうか判断できませんから! まあ、百歩譲って、それで個人的な満足を得るだけならいい。でも、たとえば恣意的なキーワードで検索して先頭付近に表示されることに満足するゲームを続けてたりすると、そのうち気分が麻痺してきて、まるでそれが真の市場の評価であるかのような錯覚に陥るものなので、ちゅういしてください。
で、何年か前にもAmazonランキングが取りざたされる状況のあいまいさにむかついて、それなら多少なりとも実際のところを検証できるようにしてやれと息巻き、Amazonランキングの推移を長期にわたってグラフにする実験をした。Amazonの書籍ページからAmazonランキングの数字を一時間に一回引っ張ってきて、それをMRTGに流し込んでるだけだけど、何年も続けてると下図のような結果が得られて興味ぶかい。基本的には会社で動かしているものなので、例としてちょっとだけ公開。グラフは、下に行くほどランキングが高くなっていることを表す。
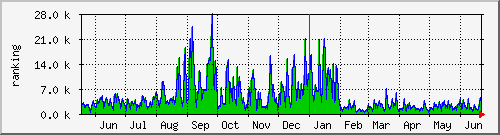
上側のグラフは、ときどき急峻な山(ランキングの落ち込み)があるけど、全体としては地を這うような傾向にある(特に今年の2月以降)。これは、ランキングとしては高値安定なので、そこそこ定番として市場に受け入れられていると思ってよさそうである。ちなみにこの本は、なにをかくそう『プログラミングのための線形代数』です。
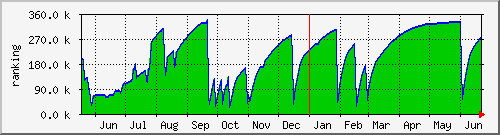
一方、下側のグラフ(書名は控えさせていただきます)は、たまに売れてランキングを戻す谷間があるけど、その間はほぼ右肩上がりの傾向にあって、だんだんランキングが下がっていることを示す。つまり、発売後しばらくは売れたかもしれないけど、定番にはならず市場から忘れられちゃって、今ではぽつぽつとだけ売れている本だと思っていい。
まあ、ようするに、バカは使えないけどデータは使いようっていう話でした。
- 社内で発行した本の販売冊数はだいたい分かるので、そのなかでのランキング
- 書店によってはランキング(もしくは実売情報)を公開しているところがあるので、そこから得られる(もしくは推測される)ランキング
- Amazon.co.jpのランキング。各書目のページに表示される数字や、特定のキーワードで検索したときに掲載される順番
もうどうしょうもないのは、1番目のランキングで高水準にある書目を見て、それが日本中でベストセラーになっているかのごとく勘違いしている場合。バカだろ。まあ、そんなケースは出版社の中にいない限りお目にかかれないけど、中にいるとしばしばお目にかかる。
2番目のランキングは、もう少し現実を反映している。でも、書店っていうのは、読者として意識している以上に得意分野と不得意分野の売り上げ差があるものだと思う。だから、特定の書店から報告されるランキングだけ目にして「○○の本は売れている」と言い放つ人は苦手だ。
いちばんイラってくるのは、3番目のランキングだけをもってあーだこーだ言われるケースである。つーか、あの「Amazonランキング」って何さ。1時間ごとに更新されるようだけど、Amazonランキングが1000だったら、少なくともその時間帯には日本で1000番目に売れている本なのか? とまあ、そういう感想が(出版社にいる以上)当然だと思うんだけど、これがぜんぜん当然じゃない。瞬間値にすぎないAmazonランキングをやたらに気にしたり、なんか適当なキーワードで検索して一番先頭に表示されることに意味を見出そうとする。そのような場当たり的な検証からは、その書籍が市場で評価されているかどうか判断できませんから! まあ、百歩譲って、それで個人的な満足を得るだけならいい。でも、たとえば恣意的なキーワードで検索して先頭付近に表示されることに満足するゲームを続けてたりすると、そのうち気分が麻痺してきて、まるでそれが真の市場の評価であるかのような錯覚に陥るものなので、ちゅういしてください。
で、何年か前にもAmazonランキングが取りざたされる状況のあいまいさにむかついて、それなら多少なりとも実際のところを検証できるようにしてやれと息巻き、Amazonランキングの推移を長期にわたってグラフにする実験をした。Amazonの書籍ページからAmazonランキングの数字を一時間に一回引っ張ってきて、それをMRTGに流し込んでるだけだけど、何年も続けてると下図のような結果が得られて興味ぶかい。基本的には会社で動かしているものなので、例としてちょっとだけ公開。グラフは、下に行くほどランキングが高くなっていることを表す。


上側のグラフは、ときどき急峻な山(ランキングの落ち込み)があるけど、全体としては地を這うような傾向にある(特に今年の2月以降)。これは、ランキングとしては高値安定なので、そこそこ定番として市場に受け入れられていると思ってよさそうである。ちなみにこの本は、なにをかくそう『プログラミングのための線形代数』です。
一方、下側のグラフ(書名は控えさせていただきます)は、たまに売れてランキングを戻す谷間があるけど、その間はほぼ右肩上がりの傾向にあって、だんだんランキングが下がっていることを示す。つまり、発売後しばらくは売れたかもしれないけど、定番にはならず市場から忘れられちゃって、今ではぽつぽつとだけ売れている本だと思っていい。
まあ、ようするに、バカは使えないけどデータは使いようっていう話でした。
2006/06/18
パズル「数独」をSchemeによる制約プログラミングで解く
SICPは3.4節の手前で足踏み中。3.3節まで練習問題はひととおり終えたけど、ここで実装しているconstraint programingの例に釈然としないものが残る。
わかんないときは自分で例を作ってみるのがいちばん。要するに
まず決めなければならないのは、「要素を何にするか」。ここではsudokuの各セルを要素として、そのセルが「取りうる数字」を考えることにする。最初は各セルとも、1〜9の数字をどれでも取りうる。
次に関係を定義する。ここでは、「各行」「各列」「各ブロック」を関係とする。「各行」「各列」「各ブロック」などをスロットと呼ぶことにすると、どのスロットも9個のセルを含み、それぞれのセルに1〜9の要素が一つずつ入らなければならない。
例えば4x4のsudokuの場合、セルは16個、スロットは12個になる。セル1〜16とスロットA〜Lの関係はこんな感じ。
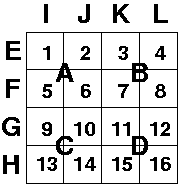
この関係についてSICPちっくなconstraint network図を描くのはやっかいだけど、無理に一部分を描けばこんな感じになると思う。
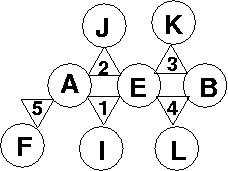
上図の関係を見ながらプロシージャを書いていく。肝心の関係の定義は、とりあえず
この関係だけでは解を求めるには不十分で、実際、これから示すコードで解けるsudokuの問題はほとんどない。
実際に問題を解いてみる。まずは初期化。トップレベルでdefineを繰り返す方法がわからない……。しかたないので、各スロットのセル一覧をリストとして出力するプロシージャで我慢して、それをトップレベルに張り付けてごまかす。
ただし、上記に書いたように最初に与えている関係が不十分なので、解は求まりきってない。
わかんないときは自分で例を作ってみるのがいちばん。要するに
- 要素間の関係を定義し、
- ある要素の値を更新すると、
- 他の要素の値も定義した関係にしたがって更新される
まず決めなければならないのは、「要素を何にするか」。ここではsudokuの各セルを要素として、そのセルが「取りうる数字」を考えることにする。最初は各セルとも、1〜9の数字をどれでも取りうる。
次に関係を定義する。ここでは、「各行」「各列」「各ブロック」を関係とする。「各行」「各列」「各ブロック」などをスロットと呼ぶことにすると、どのスロットも9個のセルを含み、それぞれのセルに1〜9の要素が一つずつ入らなければならない。
例えば4x4のsudokuの場合、セルは16個、スロットは12個になる。セル1〜16とスロットA〜Lの関係はこんな感じ。

この関係についてSICPちっくなconstraint network図を描くのはやっかいだけど、無理に一部分を描けばこんな感じになると思う。

上図の関係を見ながらプロシージャを書いていく。肝心の関係の定義は、とりあえず
- 各スロットに、まったく同じ可能性を持つセルがあったら、ほかのセルからその可能性を取り除く
この関係だけでは解を求めるには不十分で、実際、これから示すコードで解けるsudokuの問題はほとんどない。
(define (make-cell init-possibilities)
(let ((possibility init-possibilities)
(slots '()))
(define (set-my-possibility new-possibility)
(set! possibility new-possibility)
(for-each-slot possibility slots))
(define (connect slot)
(set! slots
(cons slot slots)))
(define (me request)
(cond ((eq? request 'possibility) possibility)
((eq? request 'set-possibility) set-my-possibility)
((eq? request 'connect) connect)))
me))
(define (for-each-slot possibility slots)
(cond ((null? slots) 'done)
(else
((car slots) possibility)
(for-each-slot possibility (cdr slots)))))
(define (set-possibility! cell possibility)
((cell 'set-possibility) possibility))
(define (connect cell slot)
((cell 'connect) slot))
(define (get-possibility cell)
(cell 'possibility))
(define (slot . cells)
(define (one-of-cell-has-new-possibility possibility)
(cond ((= (num-of-same-possibility possibility cells)
(length possibility))
(update-cells! cells possibility))))
(define (me possibility)
(one-of-cell-has-new-possibility possibility))
(define (connect-all-cells-to-me cells me)
(cond ((null? cells)
'done)
((connect (car cells) me)
(connect-all-cells-to-me (cdr cells) me))))
(connect-all-cells-to-me cells me)
me)
(define (update-cells! cells possibility)
(cond ((null? cells)
'slot-updated)
((or (equal? (get-possibility (car cells)) possibility)
(<= (length (get-possibility (car cells)))
(length possibility)))
(update-cells! (cdr cells) possibility))
(else
(set-possibility! (car cells)
(complement (get-possibility (car cells))
possibility))
(update-cells! (cdr cells) possibility))))
(define (complement l1 l2)
(define (include? a l)
(cond ((null? l) #f)
((equal? a (car l)) #t)
(else (include? a (cdr l)))))
(cond ((null? l1) '())
((include? (car l1) l2)
(complement (cdr l1) l2))
(else
(cons (car l1) (complement (cdr l1) l2)))))
(define (num-of-same-possibility possibility cells)
(cond ((null? cells)
0)
((equal? possibility (get-possibility (car cells)))
(+ 1 (num-of-same-possibility possibility (cdr cells))))
(else
(num-of-same-possibility possibility (cdr cells)))))
実際に問題を解いてみる。まずは初期化。トップレベルでdefineを繰り返す方法がわからない……。しかたないので、各スロットのセル一覧をリストとして出力するプロシージャで我慢して、それをトップレベルに張り付けてごまかす。
(define-syntax make9x9cellsためしに解いてみる問題としては、「数学セミナー」の2006年5月号の西川さんの記事41ページに掲載されているものを使うことにした。ちょっとみにくいけど、こんな問題。
(syntax-rules ()
((_ e)
(define e (make-cell '(1 2 3 4 5 6 7 8 9))))
((_ e1 e2 ...)
(begin
(define e1 (make-cell '(1 2 3 4 5 6 7 8 9)))
(define e2 (make-cell '(1 2 3 4 5 6 7 8 9)))
...))))
(make9x9cells
c11 c12 c13 c14 c15 c16 c17 c18 c19
c21 c22 c23 c24 c25 c26 c27 c28 c29
c31 c32 c33 c34 c35 c36 c37 c38 c39
c41 c42 c43 c44 c45 c46 c47 c48 c49
c51 c52 c53 c54 c55 c56 c57 c58 c59
c61 c62 c63 c64 c65 c66 c67 c68 c69
c71 c72 c73 c74 c75 c76 c77 c78 c79
c81 c82 c83 c84 c85 c86 c87 c88 c89
c91 c92 c93 c94 c95 c96 c97 c98 c99
)
(define s1 (slot c11 c12 c13 c14 c15 c16 c17 c18 c19))
(define s2 (slot c21 c22 c23 c24 c25 c26 c27 c28 c29))
(define s3 (slot c31 c32 c33 c34 c35 c36 c37 c38 c39))
(define s4 (slot c41 c42 c43 c44 c45 c46 c47 c48 c49))
(define s5 (slot c51 c52 c53 c54 c55 c56 c57 c58 c59))
(define s6 (slot c61 c62 c63 c64 c65 c66 c67 c68 c69))
(define s7 (slot c71 c72 c73 c74 c75 c76 c77 c78 c79))
(define s8 (slot c81 c82 c83 c84 c85 c86 c87 c88 c89))
(define s9 (slot c91 c92 c93 c94 c95 c96 c97 c98 c99))
(define s10 (slot c11 c21 c31 c41 c51 c61 c71 c81 c91))
(define s11 (slot c12 c22 c32 c42 c52 c62 c72 c82 c92))
(define s12 (slot c13 c23 c33 c43 c53 c63 c73 c83 c93))
(define s13 (slot c14 c24 c34 c44 c54 c64 c74 c84 c94))
(define s14 (slot c15 c25 c35 c45 c55 c65 c75 c85 c95))
(define s15 (slot c16 c26 c36 c46 c56 c66 c76 c86 c96))
(define s16 (slot c17 c27 c37 c47 c57 c67 c77 c87 c97))
(define s17 (slot c18 c28 c38 c48 c58 c68 c78 c88 c98))
(define s18 (slot c19 c29 c39 c49 c59 c69 c79 c89 c99))
(define s19 (slot c11 c12 c13 c21 c22 c23 c31 c32 c33))
(define s20 (slot c14 c15 c16 c24 c25 c26 c34 c35 c36))
(define s21 (slot c17 c18 c19 c27 c28 c29 c37 c38 c39))
(define s22 (slot c41 c42 c43 c51 c52 c53 c61 c62 c63))
(define s23 (slot c44 c45 c46 c54 c55 c56 c64 c65 c66))
(define s24 (slot c47 c48 c49 c57 c58 c59 c67 c68 c69))
(define s25 (slot c71 c72 c73 c81 c82 c83 c91 c92 c93))
(define s26 (slot c74 c75 c76 c84 c85 c86 c94 c95 c96))
(define s27 (slot c77 c78 c79 c87 c88 c89 c97 c98 c99))
(5)(3)( )( )(7)( )( )( )( )これらの初期値を次のように各セルに設定する。
(6)( )( )(1)(9)(5)( )( )( )
( )(9)(8)( )( )( )( )(6)( )
(8)( )( )( )(6)( )( )( )(3)
(4)( )( )(8)( )(3)( )( )( )
(7)( )( )( )(2)( )( )( )(6)
( )(6)( )( )( )( )(2)(8)( )
( )( )( )(4)(1)(9)( )( )(5)
( )( )( )( )(8)( )(1)(7)(9)
(set-possibility! c11 '(5))この時点ですべてのセルの値が更新されちゃっているのがconstraint progamingのおもしろいところ。あとは出力だけしてやればいい。
(set-possibility! c12 '(3))
(set-possibility! c15 '(7))
(set-possibility! c21 '(6))
(set-possibility! c24 '(1))
(set-possibility! c25 '(9))
(set-possibility! c26 '(5))
(set-possibility! c32 '(9))
(set-possibility! c33 '(8))
(set-possibility! c38 '(6))
(set-possibility! c41 '(8))
(set-possibility! c45 '(6))
(set-possibility! c49 '(3))
(set-possibility! c51 '(4))
(set-possibility! c54 '(8))
(set-possibility! c56 '(3))
(set-possibility! c61 '(7))
(set-possibility! c65 '(2))
(set-possibility! c69 '(6))
(set-possibility! c72 '(6))
(set-possibility! c77 '(2))
(set-possibility! c78 '(8))
(set-possibility! c84 '(4))
(set-possibility! c85 '(1))
(set-possibility! c86 '(9))
(set-possibility! c89 '(5))
(set-possibility! c95 '(8))
(set-possibility! c97 '(1))
(set-possibility! c98 '(7))
(set-possibility! c99 '(9))
ただし、上記に書いたように最初に与えている関係が不十分なので、解は求まりきってない。
(define (print-possibilities size . cells)実行結果
(let R ((ls cells) (cnt 1))
(cond ((null? ls)
'done)
((= 1 (remainder cnt size))
(newline)
(display (get-possibility (car ls)))
(R (cdr ls) (+ cnt 1)))
(else
(display (get-possibility (car ls)))
(R (cdr ls) (+ cnt 1))))))
(print-possibilities 9
c11 c12 c13 c14 c15 c16 c17 c18 c19
c21 c22 c23 c24 c25 c26 c27 c28 c29
c31 c32 c33 c34 c35 c36 c37 c38 c39
c41 c42 c43 c44 c45 c46 c47 c48 c49
c51 c52 c53 c54 c55 c56 c57 c58 c59
c61 c62 c63 c64 c65 c66 c67 c68 c69
c71 c72 c73 c74 c75 c76 c77 c78 c79
c81 c82 c83 c84 c85 c86 c87 c88 c89
c91 c92 c93 c94 c95 c96 c97 c98 c99
)
gosh> print-possibilitiesこの結果を漫然と見る限り、スロット内での重複関係を検証するだけでは解に至らないみたいだ。ここから先は、とあるセルの可能性をどちらか選択してみて、整合性がある解を探索していくしかないのだろうか?
gosh>
(5)(3)(2 4)(6)(7)(8)(9)(1 2 4)(1 2)
(6)(7)(2 4)(1)(9)(5)(3)(2 4)(8)
(1)(9)(8)(3)(4)(2)(5)(6)(7)
(8)(2 5)(9)(7)(6)(1)(4)(2 5)(3)
(4)(1 2)(6)(8)(5)(3)(7)(9)(1 2)
(7)(1 5)(3)(9)(2)(4)(8)(1 5)(6)
(9)(6)(1)(5)(3)(7)(2)(8)(4)
(2)(8)(7)(4)(1)(9)(6)(3)(5)
(3)(4)(5)(2)(8)(6)(1)(7)(9)done
2006/06/13
2006/06/10
誰も読む必要がない、ザ・日記が続きます。
朝から実家のある柏へ。レイソル戦のチケットを一緒に観戦する友人Kから受け取る。彼はゴール裏の自由席で観戦するので、試合開始の5時間も前からひたすら並んでいる。僕のほうはバックグラウンド側の指定席なので、一緒に観戦するといっても、試合中はお互いに別々の場所に陣取ることになる。ゴール裏は歌をうたったりして応援しなければならないので、つらいんですよ。
そんなわけで僕には試合開始までたっぷり時間がある。まず、彼の自転車を借りて実家へ。たまに顔を出すというのが一番難しい。主にピアノや猫と遊ぶ。それから別の旧友と待ち合わせて昼食。頼まれていた古い絵本を渡す。彼女と話をしていると、いつも、人間の面白さと社会に対する生産性とは相関しないものだと不思議に思う。いや、単純に「類は友を呼ぶ」なのかもしれない。たぶん、彼女も僕も、周囲から見ると同様に計りがたい類なんだろう。
試合開始時間がせまってきたので、あわただしく別れる。彼女は現役の柏市民だけど、ほとんどの柏市民の例に洩れず、レイソルには興味がない。なんか観戦に行く人達って遠足みたいに大きいバッグ持ってぞろぞろ歩いてるよね、とか、そういう感想がせいいっぱいらしい。
試合は楽しかった。個人的には久しぶりに勝ち試合を見ることができたし。
試合後、友人Kと合流してしばらくぶらぶらしてから、新宿の別な友人たちとの飲み会に参加して実のない一日を締めくくる。実のない会話を渾々と続けられる友人がたくさんいることが休日プレイの成否を決めると思う。そして休日プレイは生きていくのに絶対に必要な時間なわけで。
朝から実家のある柏へ。レイソル戦のチケットを一緒に観戦する友人Kから受け取る。彼はゴール裏の自由席で観戦するので、試合開始の5時間も前からひたすら並んでいる。僕のほうはバックグラウンド側の指定席なので、一緒に観戦するといっても、試合中はお互いに別々の場所に陣取ることになる。ゴール裏は歌をうたったりして応援しなければならないので、つらいんですよ。
そんなわけで僕には試合開始までたっぷり時間がある。まず、彼の自転車を借りて実家へ。たまに顔を出すというのが一番難しい。主にピアノや猫と遊ぶ。それから別の旧友と待ち合わせて昼食。頼まれていた古い絵本を渡す。彼女と話をしていると、いつも、人間の面白さと社会に対する生産性とは相関しないものだと不思議に思う。いや、単純に「類は友を呼ぶ」なのかもしれない。たぶん、彼女も僕も、周囲から見ると同様に計りがたい類なんだろう。
試合開始時間がせまってきたので、あわただしく別れる。彼女は現役の柏市民だけど、ほとんどの柏市民の例に洩れず、レイソルには興味がない。なんか観戦に行く人達って遠足みたいに大きいバッグ持ってぞろぞろ歩いてるよね、とか、そういう感想がせいいっぱいらしい。
試合は楽しかった。個人的には久しぶりに勝ち試合を見ることができたし。
試合後、友人Kと合流してしばらくぶらぶらしてから、新宿の別な友人たちとの飲み会に参加して実のない一日を締めくくる。実のない会話を渾々と続けられる友人がたくさんいることが休日プレイの成否を決めると思う。そして休日プレイは生きていくのに絶対に必要な時間なわけで。
2006/06/06
歯医者。ここ数週間というもの、抜歯した奥歯の跡をどうするかという問題に頭を悩ませていた。方法は4つ。
ブリッジでなければ、普通は入れ歯になるらしい。うーん。この年齢で入れ歯は遠慮したい。で、いっそのこと放置するのはダメなのかと聞いたら、上下左右の歯に支えがない状態になるため、虫歯はともかく歯茎の病気になりやすいくなるらしい。
というわけで、残された治療方法はインプラントしかないっぽい。インプラントは歯茎の骨に支柱を埋め込み、それに人工の歯を設置する方法で、文字通り新しい歯を一本埋め込む。したがって左右の歯を削ることもないし、かぶせものではないので普通に磨ける。ほかの歯への影響が少なく、メンテナンスが容易ってことで、やっぱり歯の治療もモジュール化が重要だな。難点は保険がきかないこと。1本につき30万円くらいみなければならないらしい。あと、僕の場合は土台になる歯茎の骨が再生するのを待たなければならないとのことで、最悪再生しない場合はブリッジをかけるしかないという問題もある。
ものすごく長いスパンで影響を及ぼすことなので、金額の問題は飲む覚悟を決めた。まあ、ぶっちゃけラップトップ一台分だと思えばいいんでしょ。あとは骨が再生するのを願うばかり。
- 放置
- 左右の歯を柱にしてブリッジをかける
- 部分入れ歯
- インプラント
ブリッジでなければ、普通は入れ歯になるらしい。うーん。この年齢で入れ歯は遠慮したい。で、いっそのこと放置するのはダメなのかと聞いたら、上下左右の歯に支えがない状態になるため、虫歯はともかく歯茎の病気になりやすいくなるらしい。
というわけで、残された治療方法はインプラントしかないっぽい。インプラントは歯茎の骨に支柱を埋め込み、それに人工の歯を設置する方法で、文字通り新しい歯を一本埋め込む。したがって左右の歯を削ることもないし、かぶせものではないので普通に磨ける。ほかの歯への影響が少なく、メンテナンスが容易ってことで、やっぱり歯の治療もモジュール化が重要だな。難点は保険がきかないこと。1本につき30万円くらいみなければならないらしい。あと、僕の場合は土台になる歯茎の骨が再生するのを待たなければならないとのことで、最悪再生しない場合はブリッジをかけるしかないという問題もある。
ものすごく長いスパンで影響を及ぼすことなので、金額の問題は飲む覚悟を決めた。まあ、ぶっちゃけラップトップ一台分だと思えばいいんでしょ。あとは骨が再生するのを願うばかり。
登録:
コメント (Atom)