パズル「数独」をSchemeによる制約プログラミングで解く

SICPは3.4節の手前で足踏み中。3.3節まで練習問題はひととおり終えたけど、ここで実装しているconstraint programingの例に釈然としないものが残る。
わかんないときは自分で例を作ってみるのがいちばん。要するに

1. 要素間の関係を定義し、
2. ある要素の値を更新すると、
3. 他の要素の値も定義した関係にしたがって更新される

という具合に「関係」ドリブンなプログラムを作ってみましょう、という話なんだよね。関係ドリブンで解にたどり着くといえば数理パズルなわけで、数理パズルといえばsudokuでしょう。constraint programingでsudokuソルバとか書けないだろうか。ふつうのsudokuソルバをどのように実装するかきちんと知らないので、もしかしたら当り前すぎてバカバカしい話かもしれないし、あるいは愚かな話なのかもしれない（ちゃんと調べること→自分）。まあ、ここはあくまでもconstraint programingの練習というスタンスで。

まず決めなければならないのは、「要素を何にするか」。ここではsudokuの各セルを要素として、そのセルが「取りうる数字」を考えることにする。最初は各セルとも、1〜9の数字をどれでも取りうる。
次に関係を定義する。ここでは、「各行」「各列」「各ブロック」を関係とする。「各行」「各列」「各ブロック」などをスロットと呼ぶことにすると、どのスロットも9個のセルを含み、それぞれのセルに1〜9の要素が一つずつ入らなければならない。

例えば4x4のsudokuの場合、セルは16個、スロットは12個になる。セル1〜16とスロットA〜Lの関係はこんな感じ。



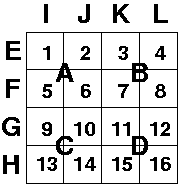
この関係についてSICPちっくなconstraint network図を描くのはやっかいだけど、無理に一部分を描けばこんな感じになると思う。



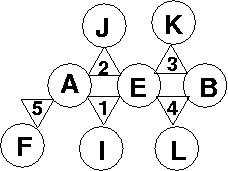
上図の関係を見ながらプロシージャを書いていく。肝心の関係の定義は、とりあえず

• 各スロットに、まったく同じ可能性を持つセルがあったら、ほかのセルからその可能性を取り除く

この関係だけでは解を求めるには不十分で、実際、これから示すコードで解けるsudokuの問題はほとんどない。

(define (make-cell init-possibilities)
  (let ((possibility init-possibilities)
        (slots '()))
    (define (set-my-possibility new-possibility)
      (set! possibility new-possibility)
      (for-each-slot possibility slots))
    (define (connect slot)
      (set! slots 
            (cons slot slots)))
    (define (me request)
      (cond ((eq? request 'possibility) possibility)
            ((eq? request 'set-possibility) set-my-possibility)
            ((eq? request 'connect) connect)))
    me))

(define (for-each-slot possibility slots)
  (cond ((null? slots) 'done)
        (else
         ((car slots) possibility)
         (for-each-slot possibility (cdr slots)))))

(define (set-possibility! cell possibility)
  ((cell 'set-possibility) possibility))
(define (connect cell slot)
  ((cell 'connect) slot))
(define (get-possibility cell)
  (cell 'possibility))


(define (slot . cells)
  (define (one-of-cell-has-new-possibility possibility)
    (cond ((= (num-of-same-possibility possibility cells)
              (length possibility))
           (update-cells! cells possibility))))
  (define (me possibility)
    (one-of-cell-has-new-possibility possibility))
  (define (connect-all-cells-to-me cells me)
    (cond ((null? cells)
           'done)
          ((connect (car cells) me)
           (connect-all-cells-to-me (cdr cells) me))))
  (connect-all-cells-to-me cells me)
  me)

(define (update-cells! cells possibility)
  (cond ((null? cells)
         'slot-updated)
        ((or (equal? (get-possibility (car cells)) possibility)
             (<= (length (get-possibility (car cells)))
                 (length possibility)))
         (update-cells! (cdr cells) possibility))
        (else
         (set-possibility! (car cells)
                           (complement (get-possibility (car cells))
                                       possibility))
         (update-cells! (cdr cells) possibility))))

(define (complement l1 l2)
  (define (include? a l)
    (cond ((null? l) #f)
          ((equal? a (car l)) #t)
          (else (include? a (cdr l)))))
  (cond ((null? l1) '())
        ((include? (car l1) l2)
         (complement (cdr l1) l2))
        (else
         (cons (car l1) (complement (cdr l1) l2)))))

(define (num-of-same-possibility possibility cells)
  (cond ((null? cells)
         0)
        ((equal? possibility (get-possibility (car cells)))
         (+ 1 (num-of-same-possibility possibility (cdr cells))))
        (else
         (num-of-same-possibility possibility (cdr cells)))))

実際に問題を解いてみる。まずは初期化。トップレベルでdefineを繰り返す方法がわからない……。しかたないので、各スロットのセル一覧をリストとして出力するプロシージャで我慢して、それをトップレベルに張り付けてごまかす。

(define-syntax make9x9cells
  (syntax-rules ()
    ((_ e) 
     (define e (make-cell '(1 2 3 4 5 6 7 8 9))))
    ((_ e1 e2 ...) 
     (begin
       (define e1 (make-cell '(1 2 3 4 5 6 7 8 9)))
       (define e2 (make-cell '(1 2 3 4 5 6 7 8 9)))
       ...))))
(make9x9cells
    c11 c12 c13 c14 c15 c16 c17 c18 c19
    c21 c22 c23 c24 c25 c26 c27 c28 c29
    c31 c32 c33 c34 c35 c36 c37 c38 c39
    c41 c42 c43 c44 c45 c46 c47 c48 c49
    c51 c52 c53 c54 c55 c56 c57 c58 c59
    c61 c62 c63 c64 c65 c66 c67 c68 c69
    c71 c72 c73 c74 c75 c76 c77 c78 c79
    c81 c82 c83 c84 c85 c86 c87 c88 c89
    c91 c92 c93 c94 c95 c96 c97 c98 c99
    )

(define s1 (slot c11 c12 c13 c14 c15 c16 c17 c18 c19))
(define s2 (slot c21 c22 c23 c24 c25 c26 c27 c28 c29))
(define s3 (slot c31 c32 c33 c34 c35 c36 c37 c38 c39))
(define s4 (slot c41 c42 c43 c44 c45 c46 c47 c48 c49))
(define s5 (slot c51 c52 c53 c54 c55 c56 c57 c58 c59))
(define s6 (slot c61 c62 c63 c64 c65 c66 c67 c68 c69))
(define s7 (slot c71 c72 c73 c74 c75 c76 c77 c78 c79))
(define s8 (slot c81 c82 c83 c84 c85 c86 c87 c88 c89))
(define s9 (slot c91 c92 c93 c94 c95 c96 c97 c98 c99))
(define s10 (slot c11 c21 c31 c41 c51 c61 c71 c81 c91))
(define s11 (slot c12 c22 c32 c42 c52 c62 c72 c82 c92))
(define s12 (slot c13 c23 c33 c43 c53 c63 c73 c83 c93))
(define s13 (slot c14 c24 c34 c44 c54 c64 c74 c84 c94))
(define s14 (slot c15 c25 c35 c45 c55 c65 c75 c85 c95))
(define s15 (slot c16 c26 c36 c46 c56 c66 c76 c86 c96))
(define s16 (slot c17 c27 c37 c47 c57 c67 c77 c87 c97))
(define s17 (slot c18 c28 c38 c48 c58 c68 c78 c88 c98))
(define s18 (slot c19 c29 c39 c49 c59 c69 c79 c89 c99))
(define s19 (slot c11 c12 c13 c21 c22 c23 c31 c32 c33))
(define s20 (slot c14 c15 c16 c24 c25 c26 c34 c35 c36))
(define s21 (slot c17 c18 c19 c27 c28 c29 c37 c38 c39))
(define s22 (slot c41 c42 c43 c51 c52 c53 c61 c62 c63))
(define s23 (slot c44 c45 c46 c54 c55 c56 c64 c65 c66))
(define s24 (slot c47 c48 c49 c57 c58 c59 c67 c68 c69))
(define s25 (slot c71 c72 c73 c81 c82 c83 c91 c92 c93))
(define s26 (slot c74 c75 c76 c84 c85 c86 c94 c95 c96))
(define s27 (slot c77 c78 c79 c87 c88 c89 c97 c98 c99))

ためしに解いてみる問題としては、「数学セミナー」の2006年5月号の西川さんの記事41ページに掲載されているものを使うことにした。ちょっとみにくいけど、こんな問題。

(5)(3)( )( )(7)( )( )( )( )
(6)( )( )(1)(9)(5)( )( )( )
( )(9)(8)( )( )( )( )(6)( )
(8)( )( )( )(6)( )( )( )(3)
(4)( )( )(8)( )(3)( )( )( )
(7)( )( )( )(2)( )( )( )(6)
( )(6)( )( )( )( )(2)(8)( )
( )( )( )(4)(1)(9)( )( )(5)
( )( )( )( )(8)( )(1)(7)(9)

これらの初期値を次のように各セルに設定する。

(set-possibility! c11 '(5))
(set-possibility! c12 '(3))
(set-possibility! c15 '(7))
(set-possibility! c21 '(6))
(set-possibility! c24 '(1))
(set-possibility! c25 '(9))
(set-possibility! c26 '(5))
(set-possibility! c32 '(9))
(set-possibility! c33 '(8))
(set-possibility! c38 '(6))
(set-possibility! c41 '(8))
(set-possibility! c45 '(6))
(set-possibility! c49 '(3))
(set-possibility! c51 '(4))
(set-possibility! c54 '(8))
(set-possibility! c56 '(3))
(set-possibility! c61 '(7))
(set-possibility! c65 '(2))
(set-possibility! c69 '(6))
(set-possibility! c72 '(6))
(set-possibility! c77 '(2))
(set-possibility! c78 '(8))
(set-possibility! c84 '(4))
(set-possibility! c85 '(1))
(set-possibility! c86 '(9))
(set-possibility! c89 '(5))
(set-possibility! c95 '(8))
(set-possibility! c97 '(1))
(set-possibility! c98 '(7))
(set-possibility! c99 '(9))

この時点ですべてのセルの値が更新されちゃっているのがconstraint progamingのおもしろいところ。あとは出力だけしてやればいい。
ただし、上記に書いたように最初に与えている関係が不十分なので、解は求まりきってない。

(define (print-possibilities size . cells)
  (let R ((ls cells) (cnt 1))
    (cond ((null? ls)
           'done)
          ((= 1 (remainder cnt size))
           (newline)
           (display (get-possibility (car ls)))
           (R (cdr ls) (+ cnt 1)))
          (else
           (display (get-possibility (car ls)))
           (R (cdr ls) (+ cnt 1))))))

(print-possibilities 9
    c11 c12 c13 c14 c15 c16 c17 c18 c19
    c21 c22 c23 c24 c25 c26 c27 c28 c29
    c31 c32 c33 c34 c35 c36 c37 c38 c39
    c41 c42 c43 c44 c45 c46 c47 c48 c49
    c51 c52 c53 c54 c55 c56 c57 c58 c59
    c61 c62 c63 c64 c65 c66 c67 c68 c69
    c71 c72 c73 c74 c75 c76 c77 c78 c79
    c81 c82 c83 c84 c85 c86 c87 c88 c89
    c91 c92 c93 c94 c95 c96 c97 c98 c99
)

実行結果

gosh> print-possibilities
gosh>
(5)(3)(2 4)(6)(7)(8)(9)(1 2 4)(1 2)
(6)(7)(2 4)(1)(9)(5)(3)(2 4)(8)
(1)(9)(8)(3)(4)(2)(5)(6)(7)
(8)(2 5)(9)(7)(6)(1)(4)(2 5)(3)
(4)(1 2)(6)(8)(5)(3)(7)(9)(1 2)
(7)(1 5)(3)(9)(2)(4)(8)(1 5)(6)
(9)(6)(1)(5)(3)(7)(2)(8)(4)
(2)(8)(7)(4)(1)(9)(6)(3)(5)
(3)(4)(5)(2)(8)(6)(1)(7)(9)done

この結果を漫然と見る限り、スロット内での重複関係を検証するだけでは解に至らないみたいだ。ここから先は、とあるセルの可能性をどちらか選択してみて、整合性がある解を探索していくしかないのだろうか？